However as a mathematical model is restricted by the limitations of set theory we have
EMCSR | 2014
Book of Abstracts | 405-408
ISSN 2227-7803
BCSSS
The system as emergent process
in Topos Theory
Michael Heather
Northumbria University, Newcastle NE2 1XE, UK,
michael.heather@trinity.cantab.net;
http://www.computing.unn.ac.uk/staff/CGNR1/
Nick Rossiter
Northumbria University, Newcastle NE2 1XE, UK,
nick.rossiter1@btinternet.com
http://www.computing.unn.ac.uk/staff/CGNR1/
Keywords: Emergence; Design; Open System Theory; Open Holistic Systems; Life Systems; Process;
Topos Theory; Category Theory; Cartesian Closed Category; Adjointness; Terminal Object; Category of
the Ultimate; Quantum Reality; Robert Rosen; Alfred North Whitehead.
1 Overview
Emergence is a fundamental component of the current understanding of science but as a
‘top-down’ holistic mechanism it would be a contradiction in terms to call it foundational.
Emergence describes the global devolution of the world everywhere adjoint to local
evolution. Emergence is often as at this EMCSR meeting bracketed with the word ‘design’.
To grasp a rigorous understanding of these twin terms as part of science they need to be
expressed as formal concepts. Systems Theory hardly justifies its existence as a theory if it
cannot be expressed formally. Formal definitions are not always easy and particularly
difficult when they lie at the cutting edge of science in terra incognita. Emergence is usually
treated as a process and design as possessing an open structure. Words like ‘process’ ,
‘structure’, and ‘open’ more fortunately do have a track record to draw on.
Emergence as allied to design belongs to open system theory. It is the process that comes
out of ‘openness’. To be scientific systems theory has to be underpinned by rigorous logic.
Classical logic tends to be stuck in closed systems and does not avail much for open
systems. Yet open systems comprise the vast majority of problems in current areas that
system theory is today called to address. The logic of openness is by its very nature the
logic of the third way. Such logic is very difficult to represent in classical logic because
classical logic is Boolean and only operates two-way. We earlier drew attention to the
difficulties even to define ‘open systems’1 let alone to understand them formally. A cause
célèbre for emergent design is to explain the existence of life. The pioneer a way ahead of
his time in the study of life systems was Robert Rosen who recommended a shift from set
theory to category theory:
“the natural habitat for discussing . . . specific modelling relations”. (Rosen 1991 p 153)
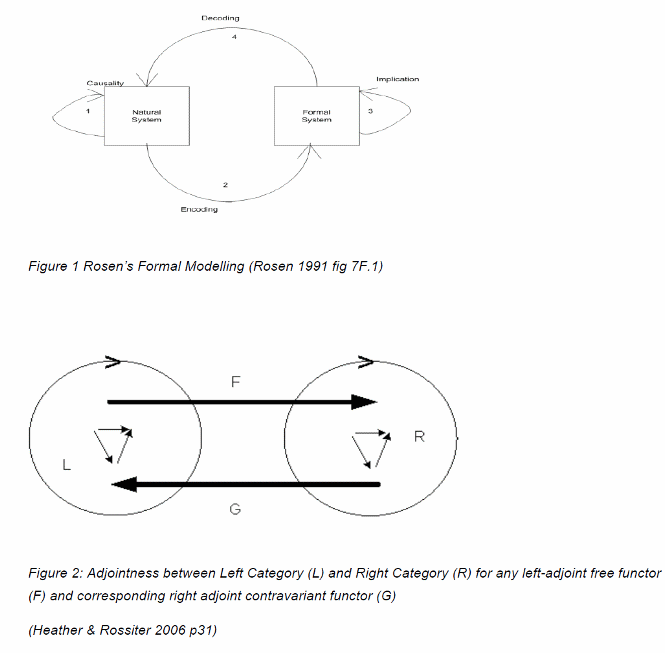
Rosen’s informal diagram is reproduced in figure 1. Emergence is in effect the ‘implication’2
on the right of his diagram. We followed Rosen’s prescription for category theory to express
the logic of social systems3 . It turns out that Rosen’s informal diagram was an early
attempt to represent the archetypal process of universal adjointness in a cartesian closed
category as shown between any two categories in our corresponding formal diagram of
figure 2. This shows the contravariant free and underlying functors between the left and
right structures. Given any one of these fixes the other three uniquely when expressed this
way. Therefore a particular right structure emerges by a particular choice of the free functor
(F). This is both awesome and trivial in that every choice we make determines the next
unique state of the world.
1 See, Heather & Rossiter (2006)
2 In Rosen’s context ‘implication’ was the emergence of life.
3 See, Heather & Rossiter (2008)

However
as a mathematical model is restricted by the limitations of set
theory we have
found it necessary to follow Alfred North Whitehead in his seminal work on Process &
Reality and ascend up two levels from models to metaphysics4. This brings us to the
highest possible level of category theory which is topos theory. The topos like the category
is another of Aristotle’s insights. From a conventional ‘bottom-up’ approach this is a terminal
object but in the reality of quantum theory it is the starting point. The topos is the formal
structure where every entity effects every other entity directly and indirectly through every
other object, which describes the structure of the physical Universe. Grothendieck of the
anarchic Bourbaki group of mathematicians in France was possibly the first to grasp the
concept of the topos as a ‘mathematical universe of universes’. However that is one level
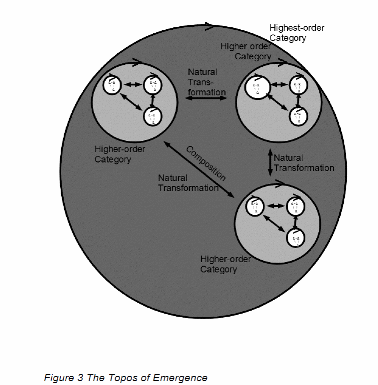
too short to reach the level of Whitehead’s metaphysics. We need to go up to the category
of category of categories (the level of the double power set in naive set theory) to reach the
top level of closure, the topos as in figure 3. Here there are the three levels of category.
The double headed arrow represents the pair of contravariant functors as in figure 2. Also
such a pair exists between each level. Consequently the left to right structure of figure 2
represents the process of emergence.
4 See, Heather & Rossiter (2014).
References
Heather, Michael, & Rossiter, Nick, (2008). The Logic for Social Systems, EMCSR-2008: European
Meeting on Cybernetics and Systems Research, Symposium Sociocybernetic Models: Conceptual
and Formal Approaches, University Vienna, 25-28 March II 653-658
Heather Michael & Rossiter Nick, (2014) Formal Representation of Process & Reality in the
metaphysical language of Category Theory: Whitehead's relational theory of space (in the press)
Rosen, R, (1991) Life Itself, A Comprehensive Inquiry into the Nature, Origin, and Fabrication of Life
Columbia University Press, New York
Rossiter, Nick, & Heather, Michael, (2006) Free and Open Systems Theory, EMCSR-2006,
Cybernetics and Systems, 18th European Meeting on Cybernetics and Systems Research,
University of Vienna, 18-21 April 2006, Trappl, R, (ed) 1 27-32
About the Authors
Michael Heather and Nick Rossiter have collaborated on over 150 papers in the theory of information
systems and related topics, concentrating mainly in the application of category theory.